The Internet is a fire hose of high pressure data. Your brain is processing, and categorizing, and grouping things as fast as it can- but it isn't fast enough.

The computer was designed to augment the human mind, not the other way around. Why do I have to teach it where to place bookmarks, how to group tabs, and where to store my data?

Why can't a computer automatically group tabs, bookmarks, notes, and more…?

Well, actually, it can! Nyxt is now available with automatic grouping! (Also known as clustering.) Let the computer group your tabs, bookmarks, and more. Focus on what matters, let the machine handle the fire hose.

How to use it?

Our first application of clustering can be seen in list-buffers. Invoke list-buffers with :cluster t (you can use execute-extended-command to interactively specify arguments to commands).

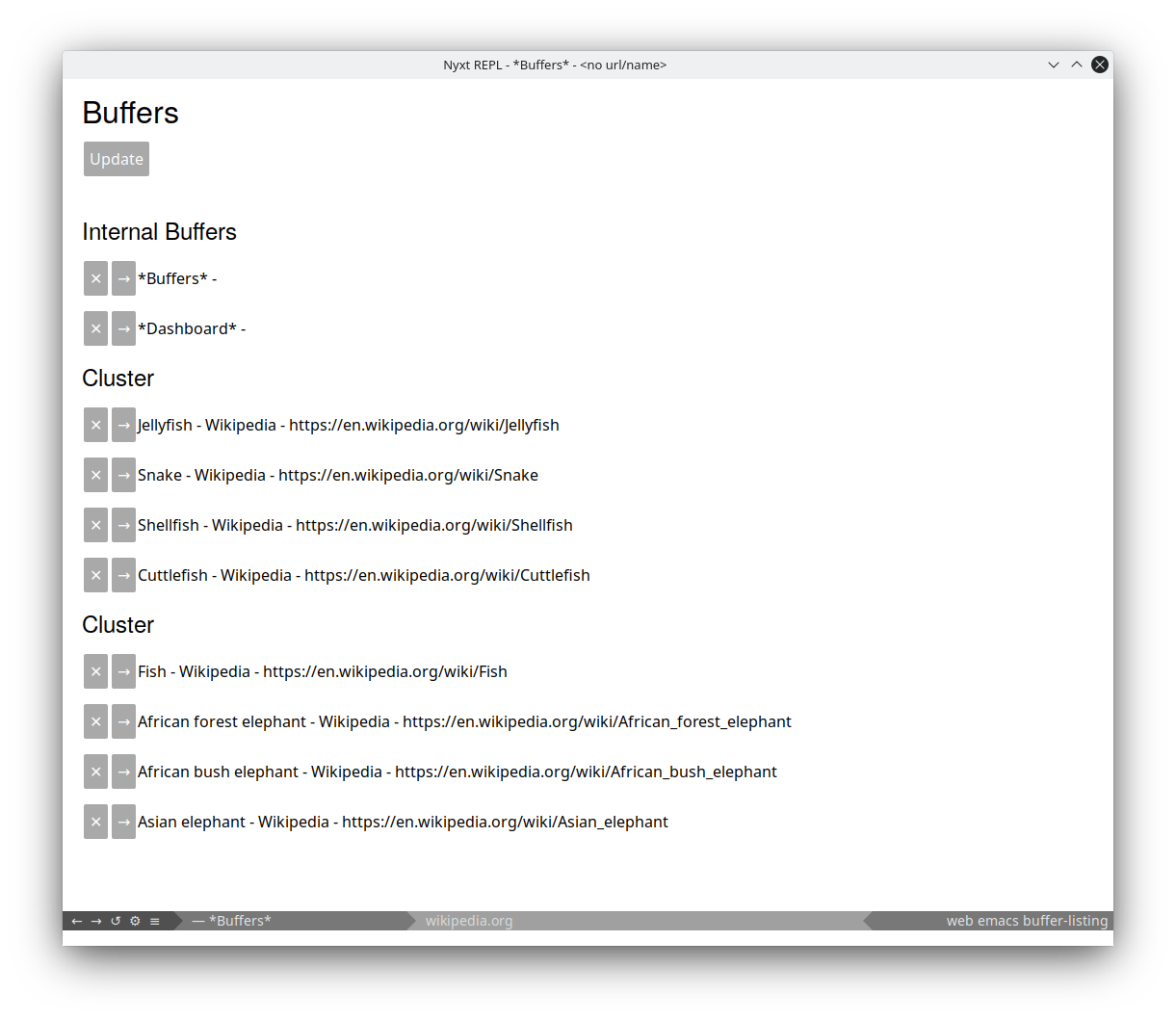
Et voila! Great, but not perfect! We are still tuning the feature extraction. We expect improvement in future iterations!

To get started utilizing clustering in your extensions (unstable API), you can:

1. Make a analysis::document-collection object.
2. Add analysis::document-cluster objects to your collection.
3. Then, invoke the following incantations:

(analysis::tf-vectorize-documents collection)
(analysis::generate-document-distance-vectors collection)
(analysis::dbscan collection :minimum-points 3 :epsilon 0.065)
(analysis::clusters collection)

The final line: (analysis::clusters collection) will return a hash table with each key representing a cluster, and the value being a list of objects in that cluster.

How does a computer group things?

There are many algorithms for clustering (grouping) data. In Nyxt, we chose Density-based spatial clustering of applications with noise (DBSCAN) as our general purpose clustering algorithm. We chose DBSCAN because:

• it can deal with an unspecified quantity of clusters,
• it is good at handling noisy data sets (the Internet is very noisy),
• it can handle clusters of any shape.

DBSCAN is far more straightforward than it sounds. Here is an image from Wikipedia showing a graphical representation of the algorithm in action. (By Chire - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=17045963):

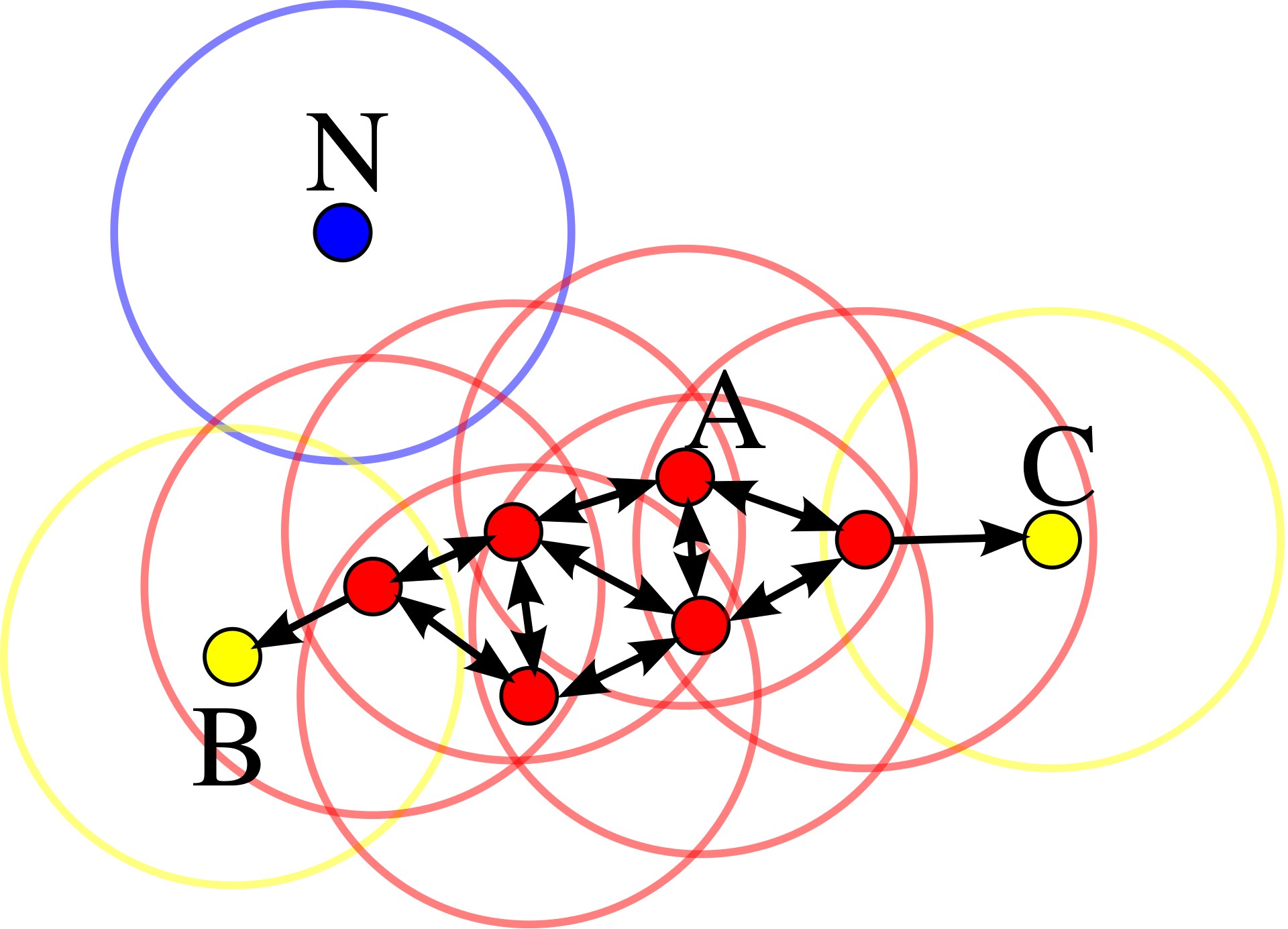
In the above graphic we can see three different colors, red, blue, and yellow.

• Red represents a core point: a point with four or more points close by.
• Yellow represents a regular point: a point close to a core point.
• Blue represents a noise point: a point not close enough to a core point or regular point.

DBSCAN can be tuned in different ways. You can specify a minimum number of points needed nearby a "core" point (typically specified as minPts). You can also specify what the distance of a 'close point' should be (typically specified as ε).

Wikipedia provides a succinct explanation of how the algorithm works:

1. Find the points in the ε (eps) neighborhood of every point, and identify the core points with more than minPts neighbors.
2. Find the connected components of core points on the neighbor graph, ignoring all non-core points.
3. Assign each non-core point to a nearby cluster if the cluster is an ε (eps) neighbor, otherwise assign it to noise.

If you need more information, the Wikipedia page is a recommended good starting point: https://en.wikipedia.org/wiki/DBSCAN.

How can we measure the distance between two buffers?

As demonstrated, clustering algorithms like DBSCAN only work when we can measure the distance between two objects. Therefore, to group buffers, we need to calculate a distance between them.

On a very abstract level, in order to measure the distance between two buffers, we convert the text of the buffer into a vector (a single dimensional array). Each index in the array represents a word, and the value represents the importance of that word in the text. We then measure the Euclidean distance between any two vectors (buffers) https://en.wikipedia.org/wiki/Euclidean_distance.

What are the implications?

We have just cracked open the lid of Pandora's data processing box. We believe that computer aided data processing will help augment users to tame the fire hose of data that is the Internet. It will lead to greater understanding of data, deeper insights into knowledge bases, and more. We foresee many applications, refinements, and tasks that will be greatly simplified through the great power that lies just beneath your fingertips. We hope you join us on this journey.

Thanks for reading :-)